Decision Making for Robotics

Mini Project 1:

Blossom Algorithm

Authors: Achal Vyas and Pruthvi Sanghavi

Summary

Blossom Algorithm is a matchmaking algorithm used to produce a maximum matching on any graph. It was created by Jack Edmunds in 1961[9]. It has applications in a wide variety of fields of Robotics, Operations Theory, Biology, Mathematics etc. In this article, we will focus our attention on the applications in the domain of Robotics and Decision Making for Robotics. A matching is a graph that occurs when all vertices are connected to at most one other vertex through a single edge. A maximum matching occurs when the number of edges in the matching graph is maximized.
Before we dive deeper into the intrinsics of the algorithm. First we will discuss, what is graph theory[6][7] and its basic elements -


Graph theory: is the field of mathematics that deals with mathematical structures used to model pairwise relationships between objects.

Graph:A Graph G is an ordered pair of disjoint sets G = (V, E) where E => VxV. Set V is called the vertex or the node set and Set E is called the edge set of graph G.

Vertex:A fundamental unit with which a graph is constructed.

Edges:The objects which connect the vertices to form a graph.

Path:A path is a sequence of vertices traversed using edges.

Augmenting Path:An augmenting path starts and ends at a free vertex and alternates between unmatched and matched edges.

A Graph is represented by a set of vertices and the edges connecting these vertices. The true essence of the graph theory is its flexibility with which it can be used to model a wide variety of problems. A Graph is used in the domain of computer science to model communication networks, data strucures, computer organizations and flow of computations in the field of sociology to measure actors' prestige or to explore rumor spreading and in the field of Robotics to model multi robotics problem and task allocation problems. The Travelling Salesman Problem is an optimization problem and it can be used using the techniques applied to solve the problems in graphs. In multi robot applications, robots and the task space are modelled as a graph and a matching algorithm is used to allot the specific task to the robot.

Visualizing the Algorithm

The visualization of the algorithm is produced using TU Munich' Edmond's Blossom Algorithm Visualizer [7]

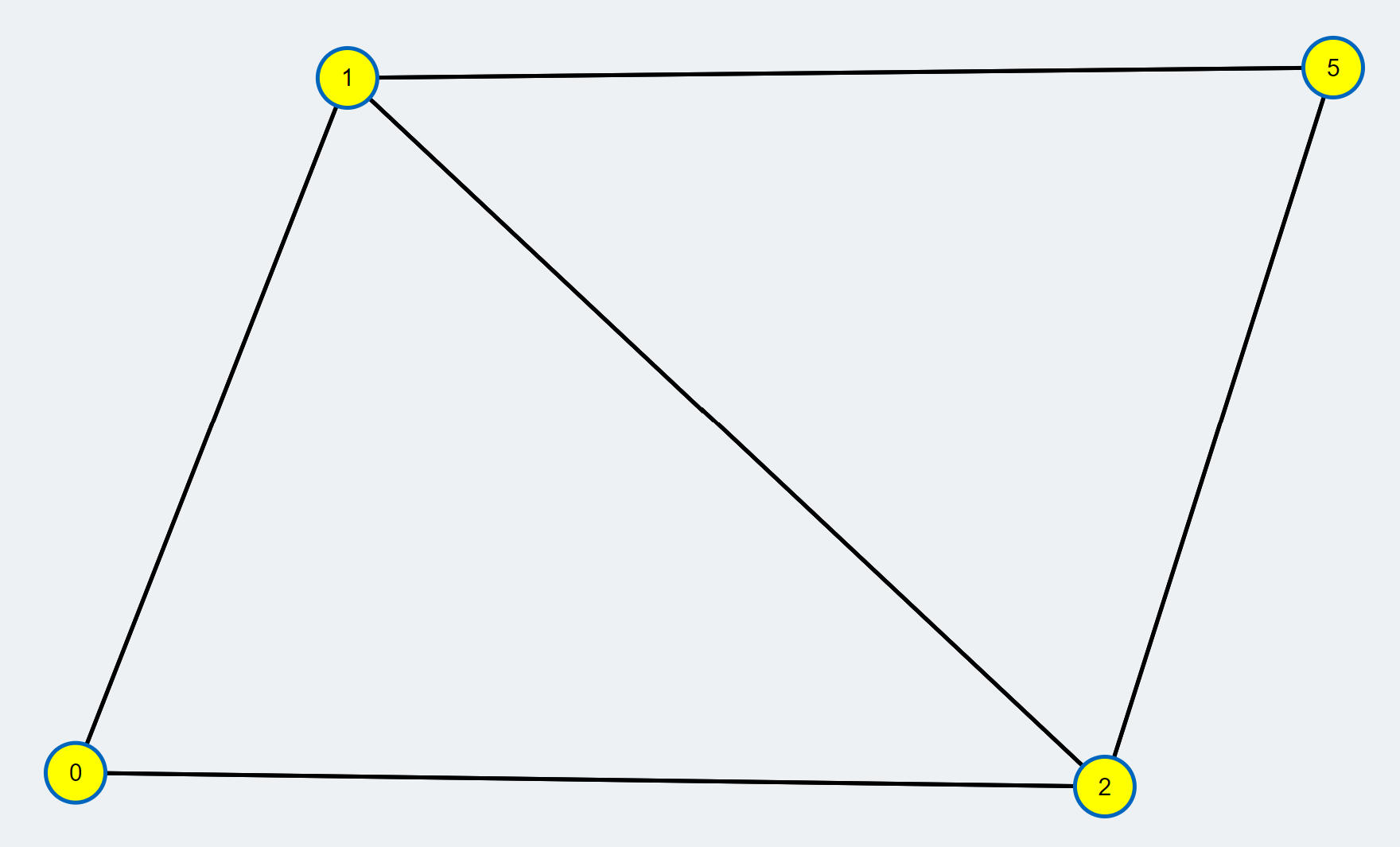
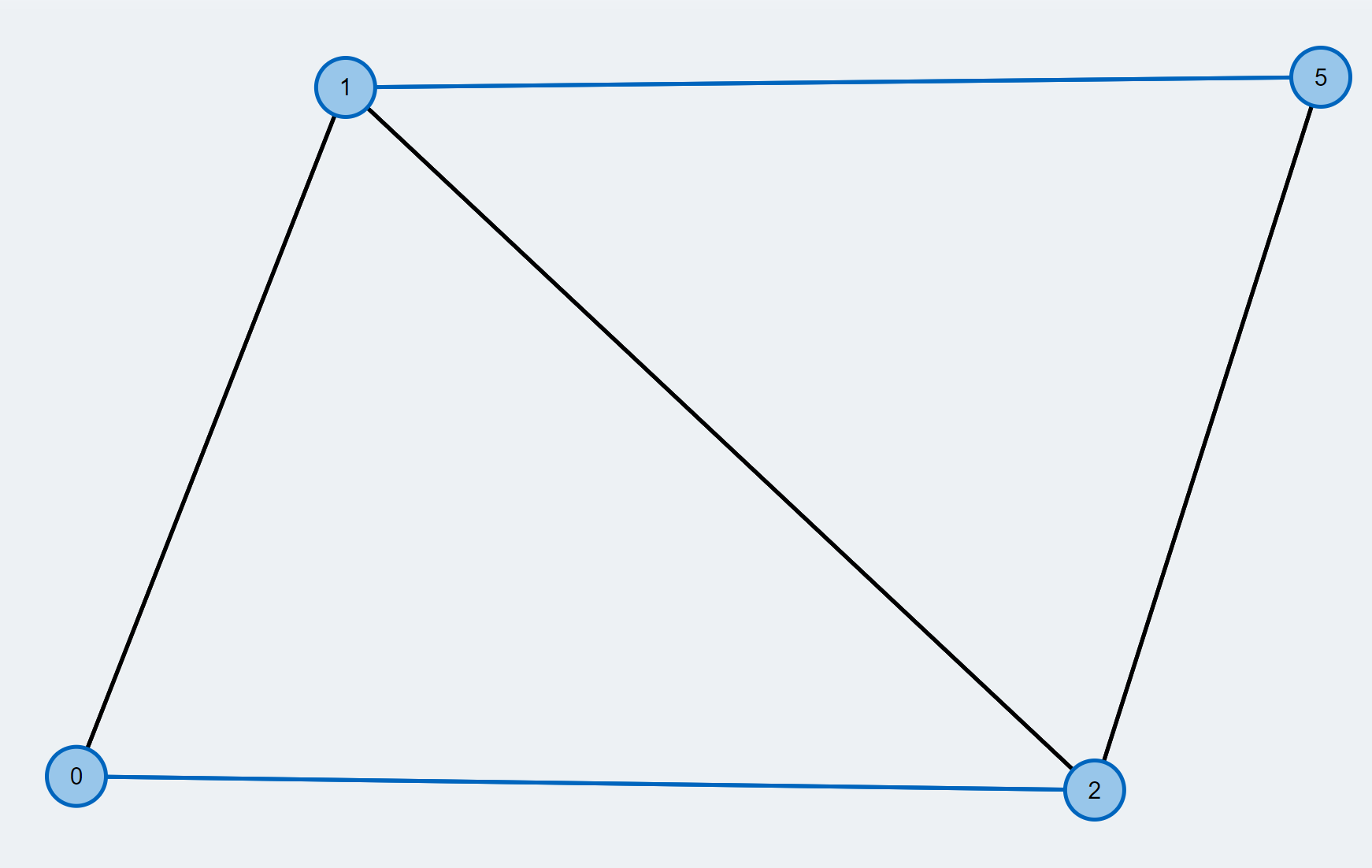
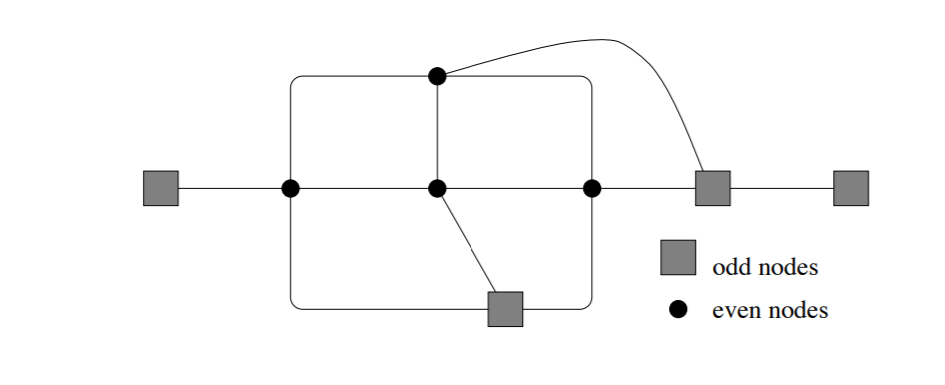
Consider an undirected graph G as shown in the graphic.

1. All the vertices are unmatched(free vertices) as shown in yellow. An augmenting path can be found to improve matching

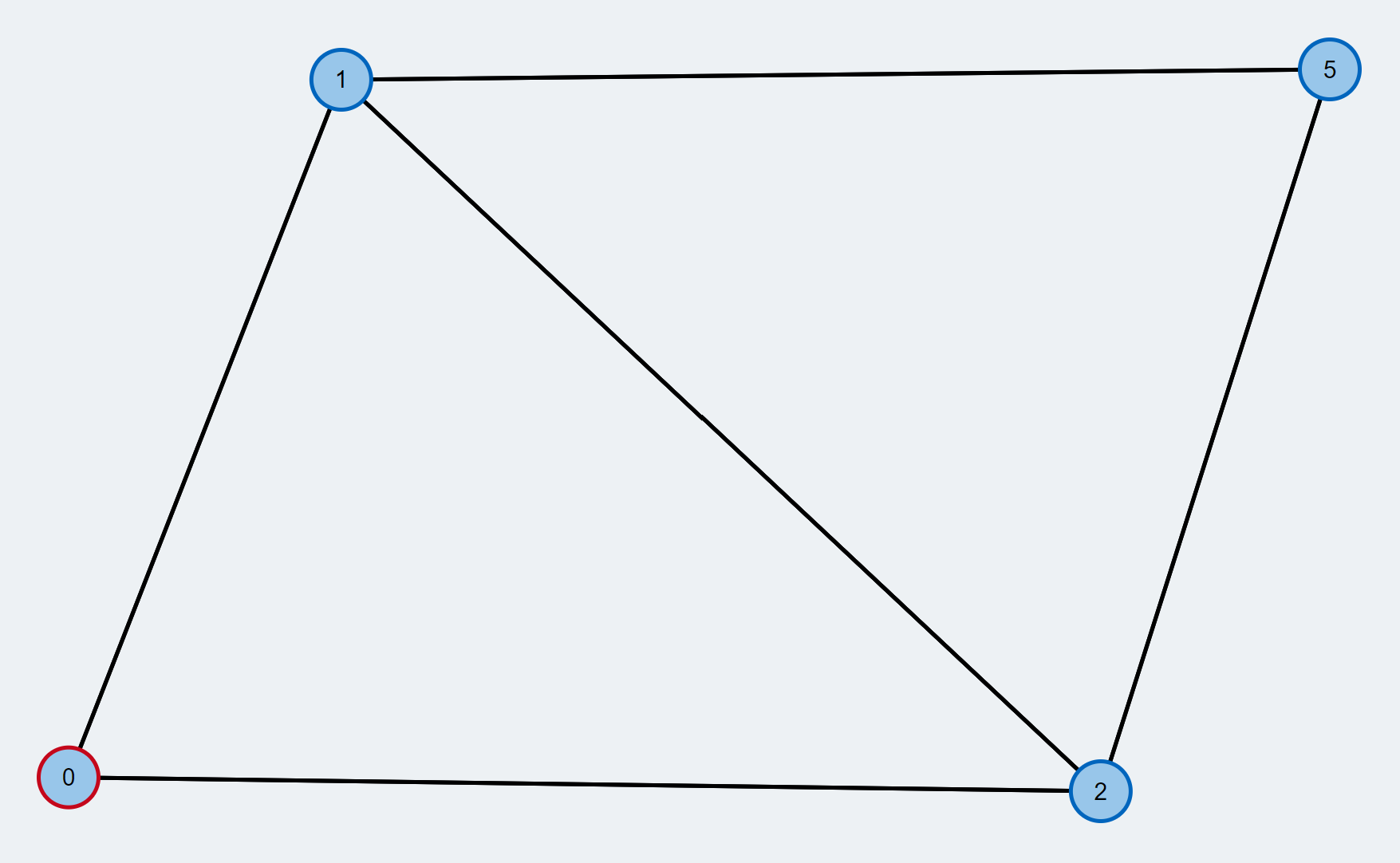
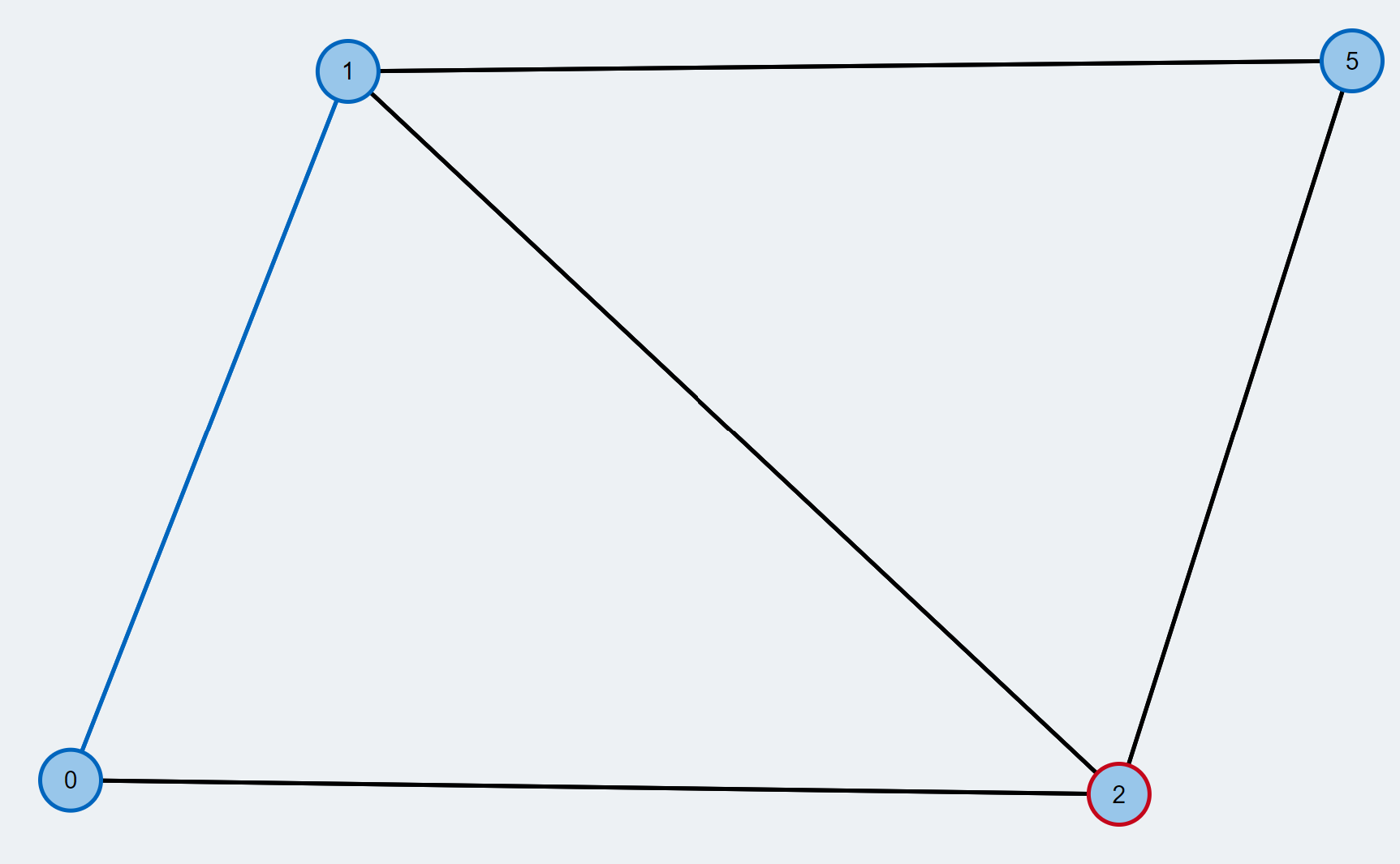
2. A node is selected and assigned as the root node(red). A Breadth first search is initiated from the node. A tree of alternating path is expanded until the we reach another free vertex

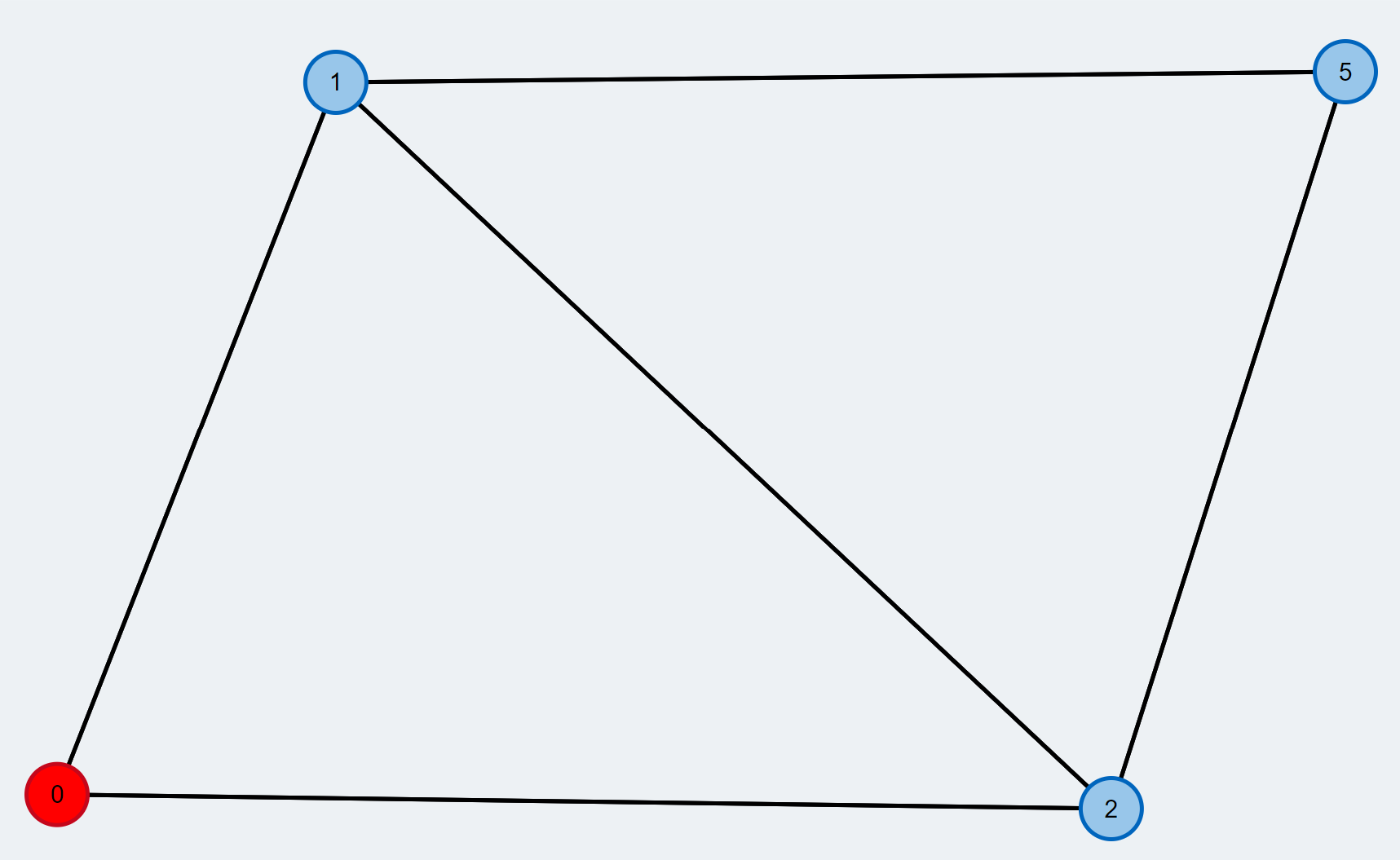
3. A node is chosen from the queue and assigned as the active node (red) and its neighbours are explored to look for the free vertex

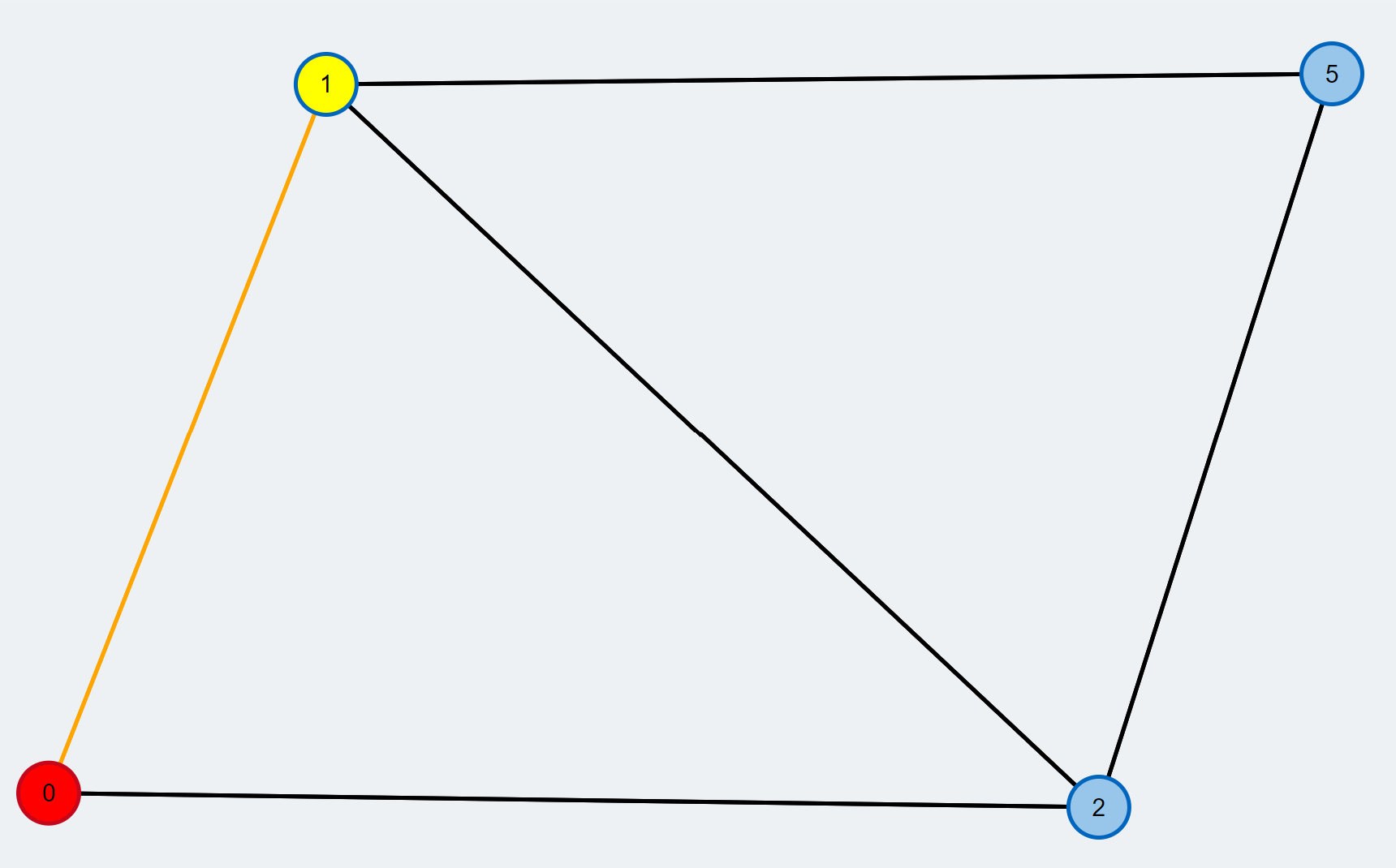
4. The next neighbouring node (orange edge) is checked and if the next node is free(yellow), then there is an augmenting path between the current root and the new node

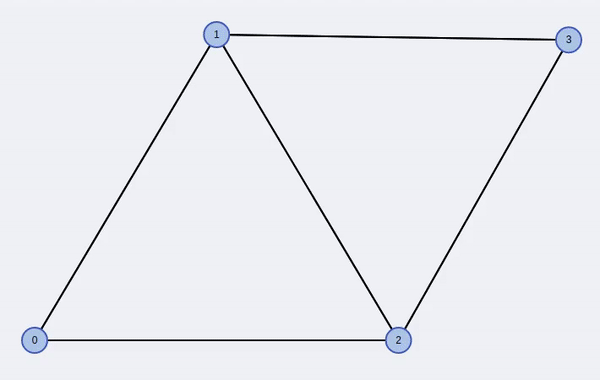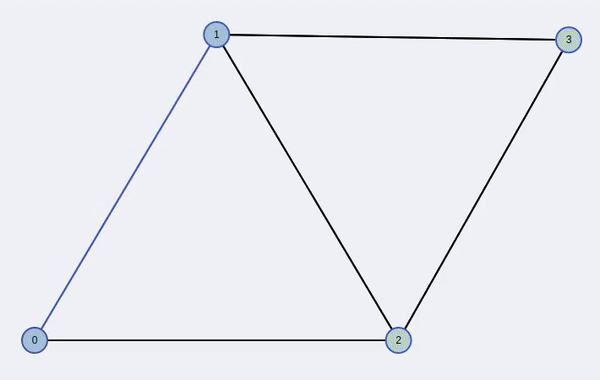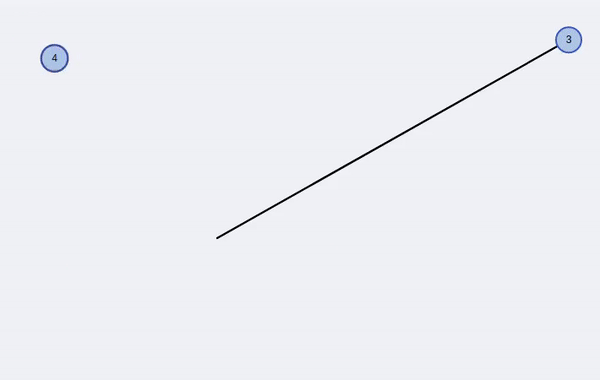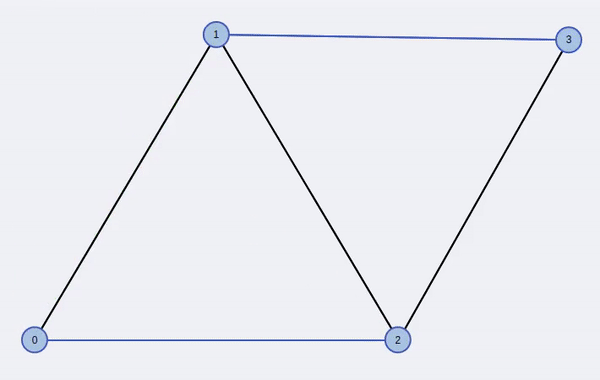
5. The augmenting path is reconstructed and is highlighted as green

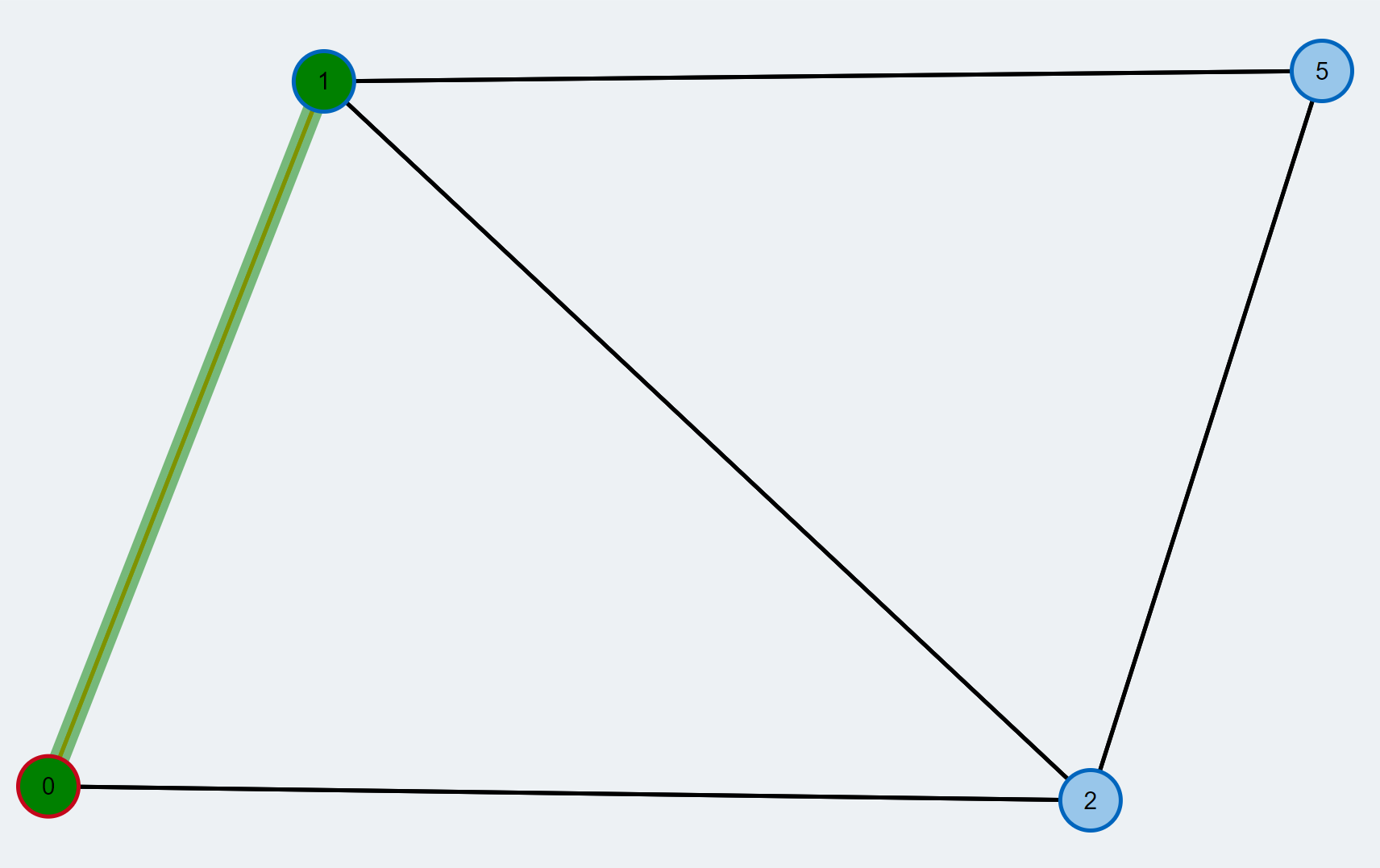
6. The augmenting path is inverted to improve the matching. Inverting an augmenting path means that all unmatched edges along the path are changed to matched ones and vice versa. By doing so, the number of edges contained in the matching increases by 1. The new matching is colored blue.

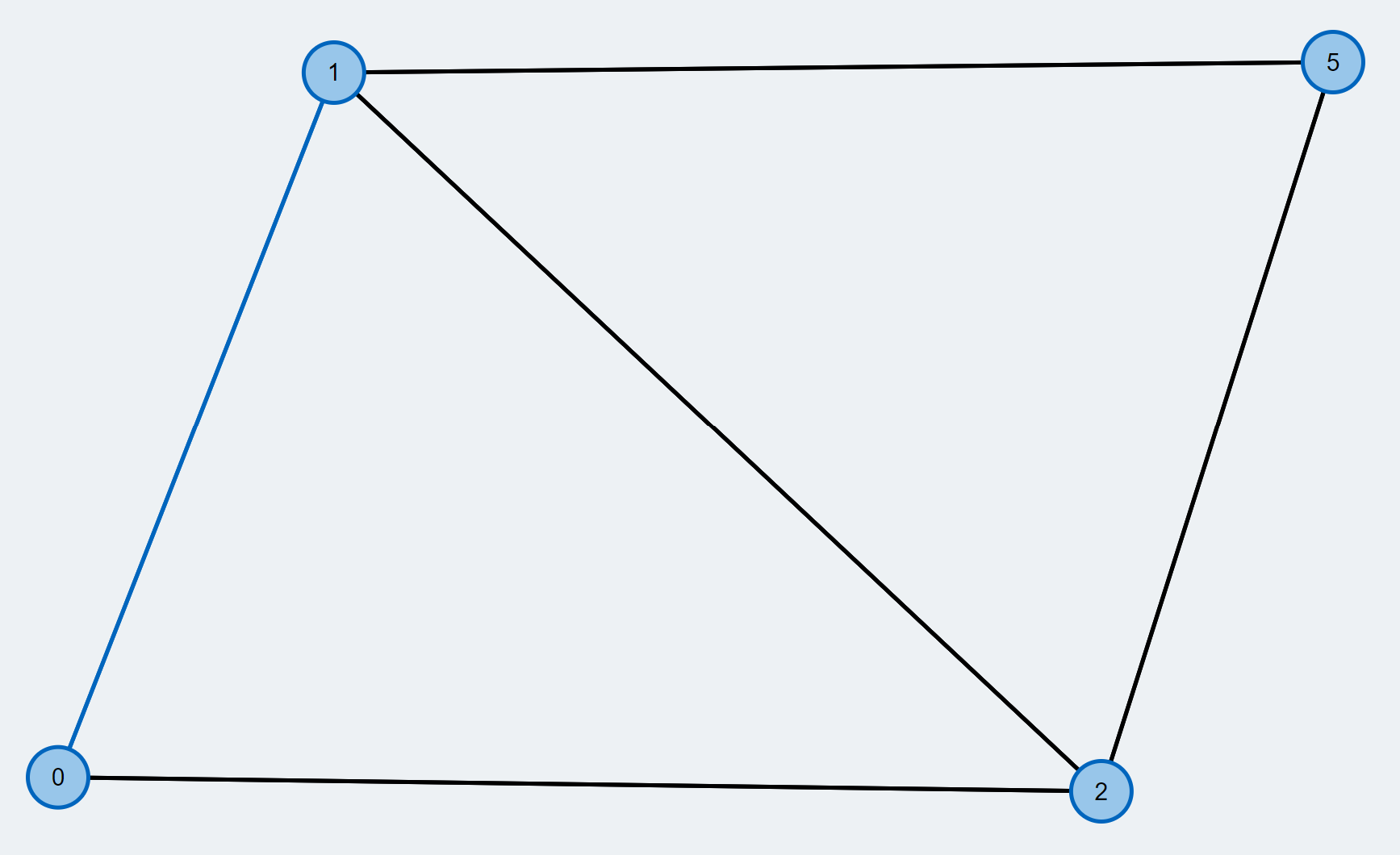
7. There are still unmatched vertices (yellow). We call them free vertices. We try to find an augmenting path to improve the matching. An augmenting path starts and ends at a free vertex and alternates between unmatched and matched edges.

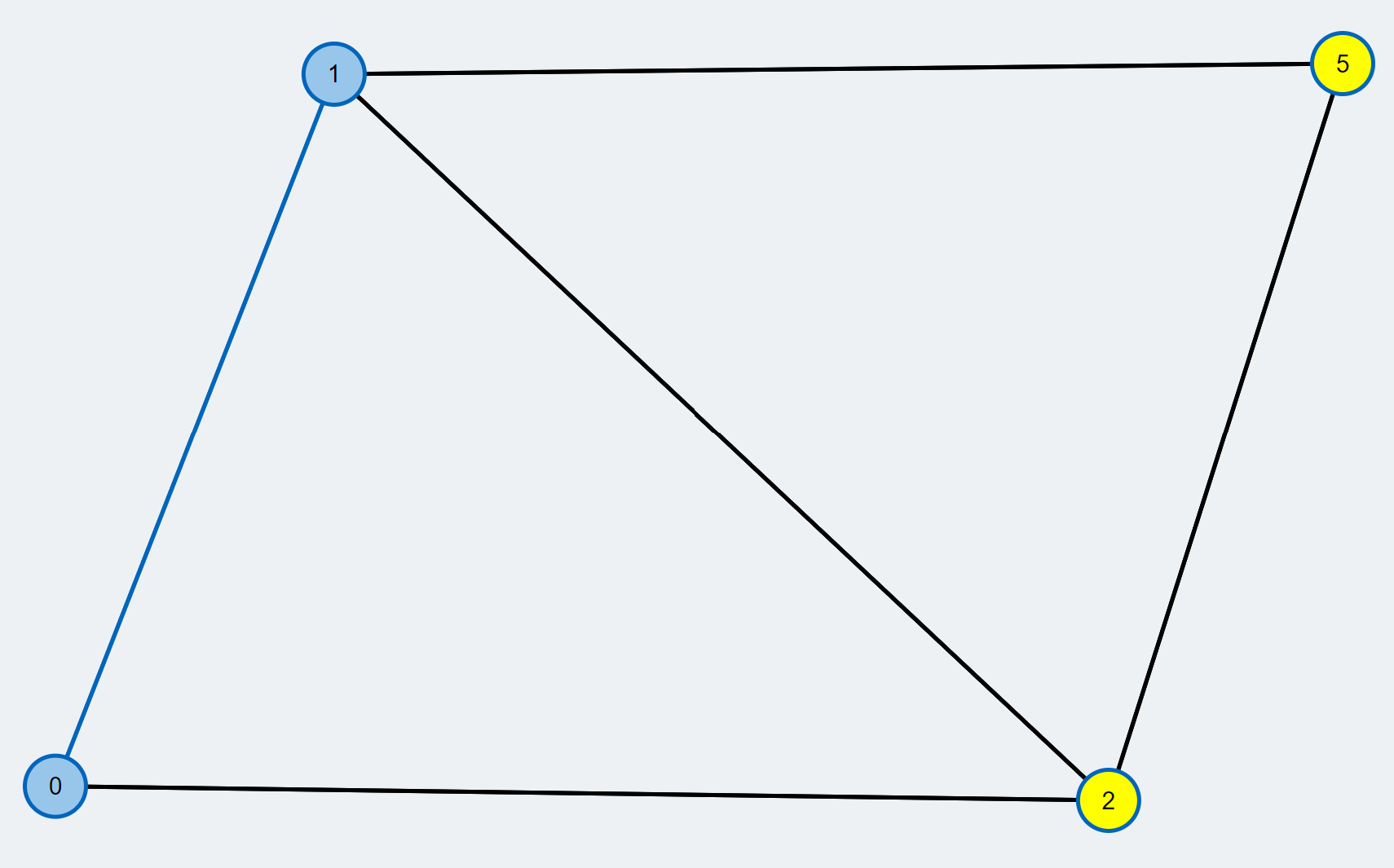
8. We pick one of the free vertices as the root node of a modified Breadth-First Search (BFS). Its stroke is colored red throughout the execution of the BFS. From the root node, we will construct a tree of alternating paths (BFS tree) until we reach another free vertex.

9. Pick the next node from the BFS queue. We call this node the currently active node and color it red. From this node, we will explore its neighbors to look for a free vertex.

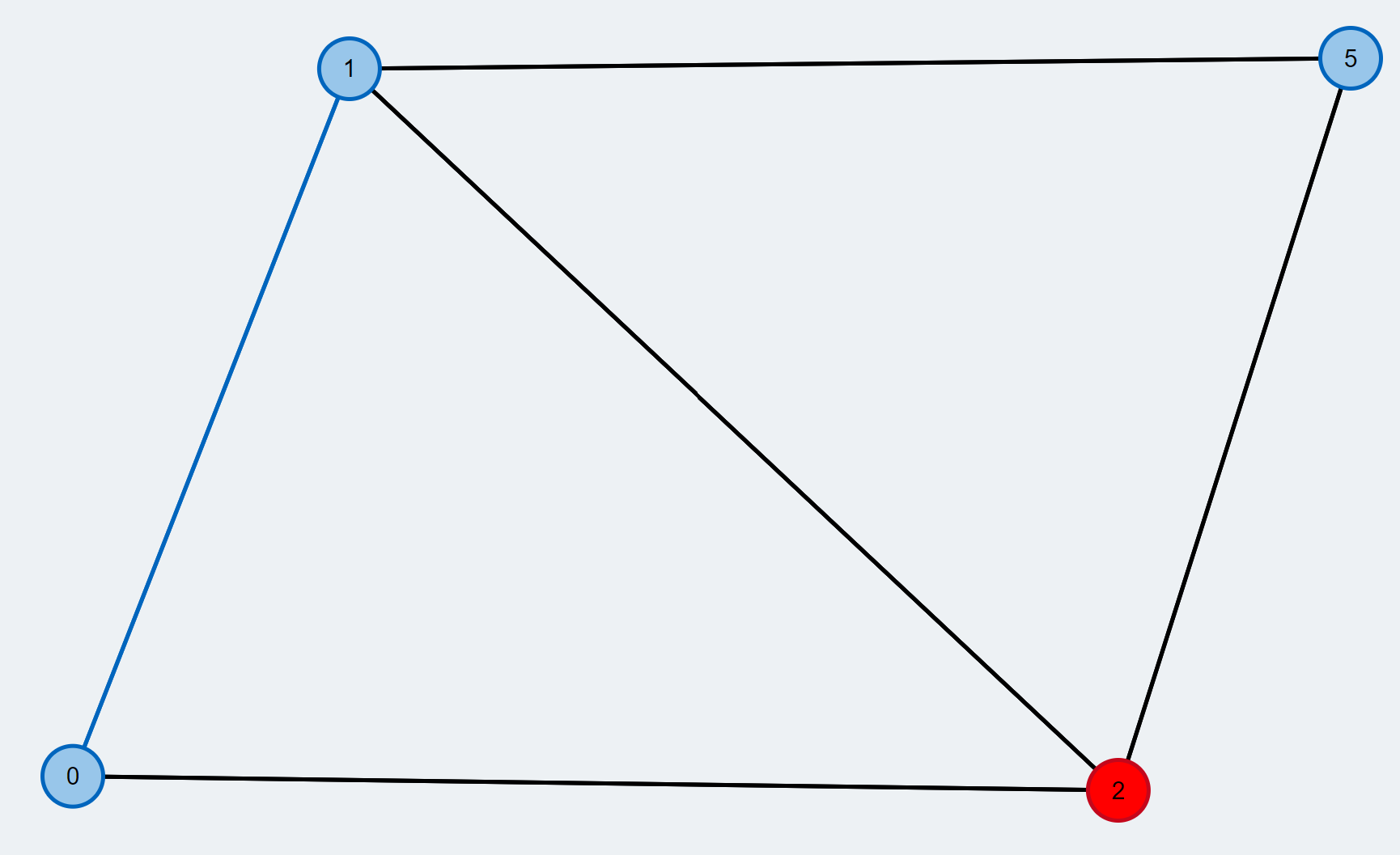
10. We check the next neighbor (orange) and find that it is already matched.

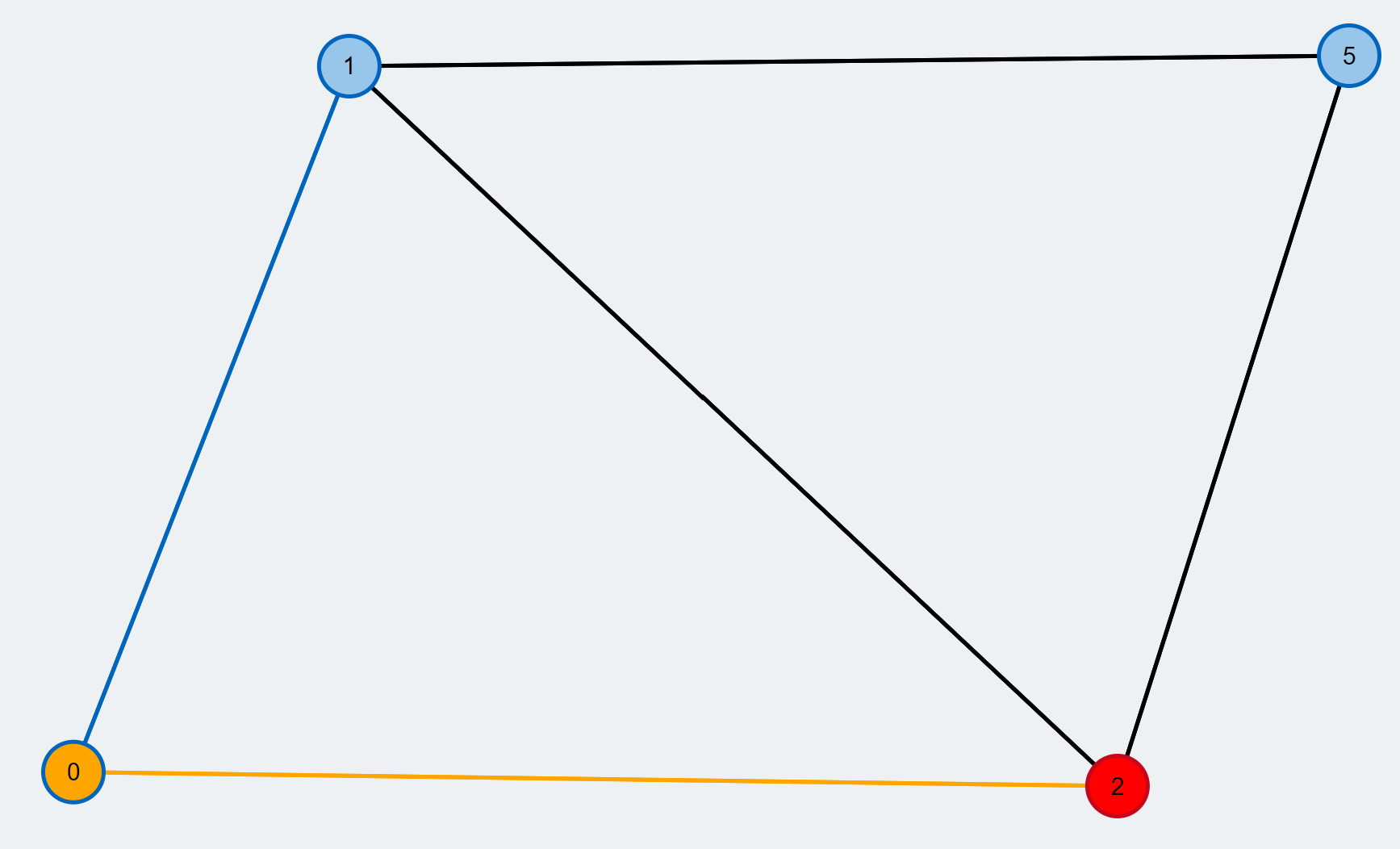
11. We add the neighbor and its mate to the BFS tree. The mate is further pushed to the BFS queue and we might continue our search from there later. The edges of the BFS tree are highlighted by a grey overlay.

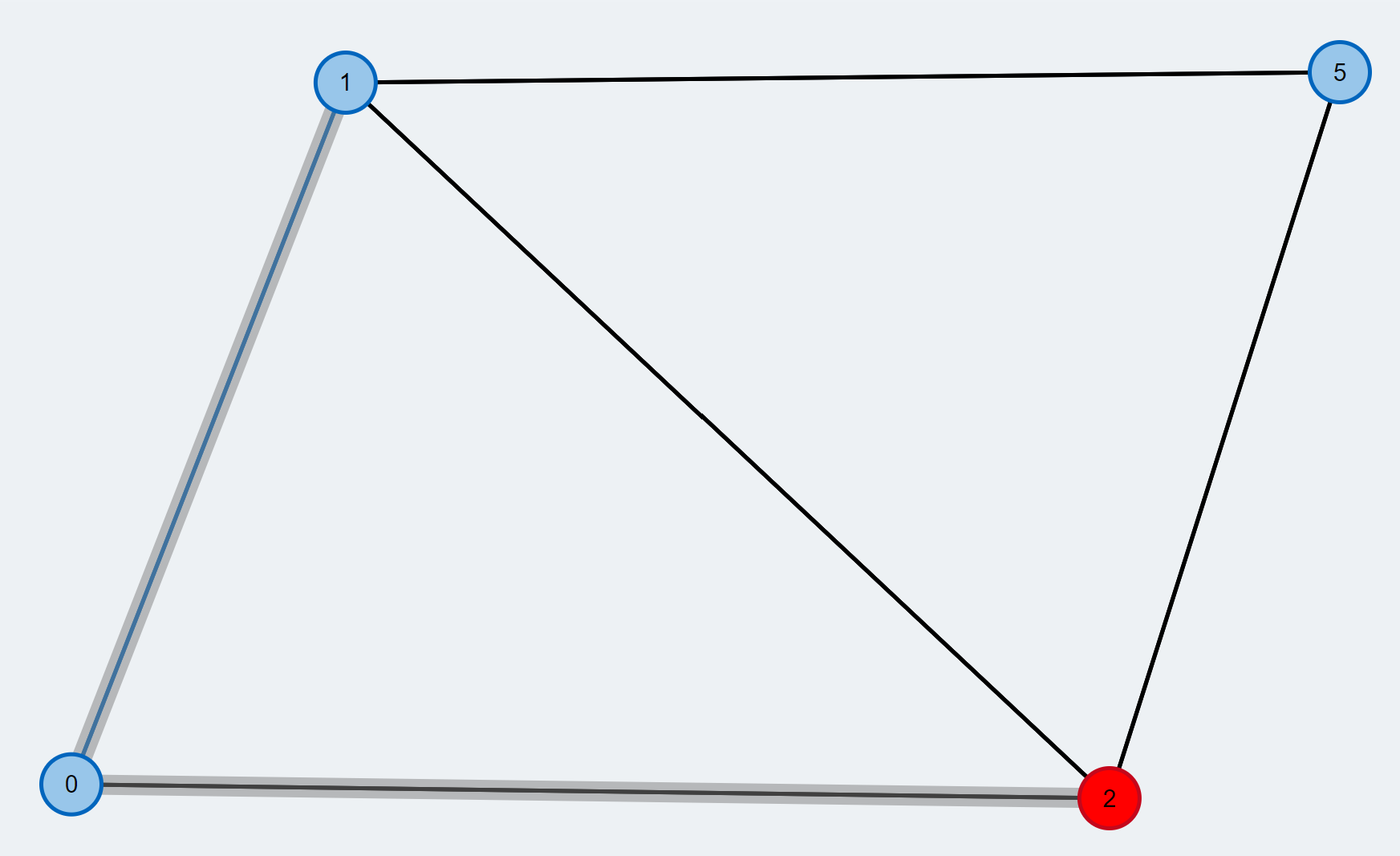
12. We check the next neighbor (orange) and find that this node is already contained in the BFS tree. Thus, there exists a cycle and we see that it has an odd number of edges. We call such a cycle a blossom.

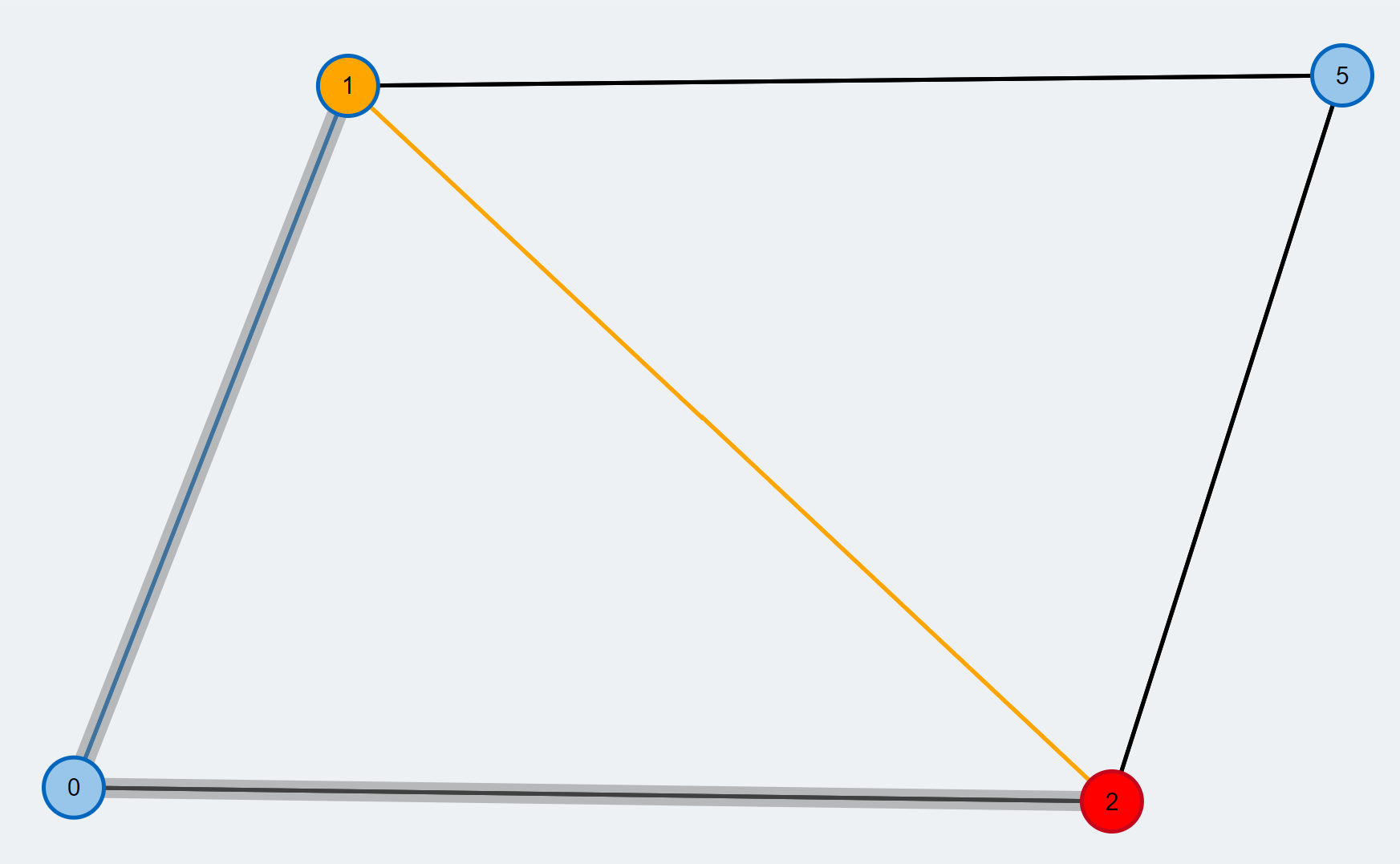
13. The odd-length cycle we found is contracted to a single supernode. Supernodes are highlighted by a larger radius compared to the other nodes. We further push the new supernode to the BFS queue.

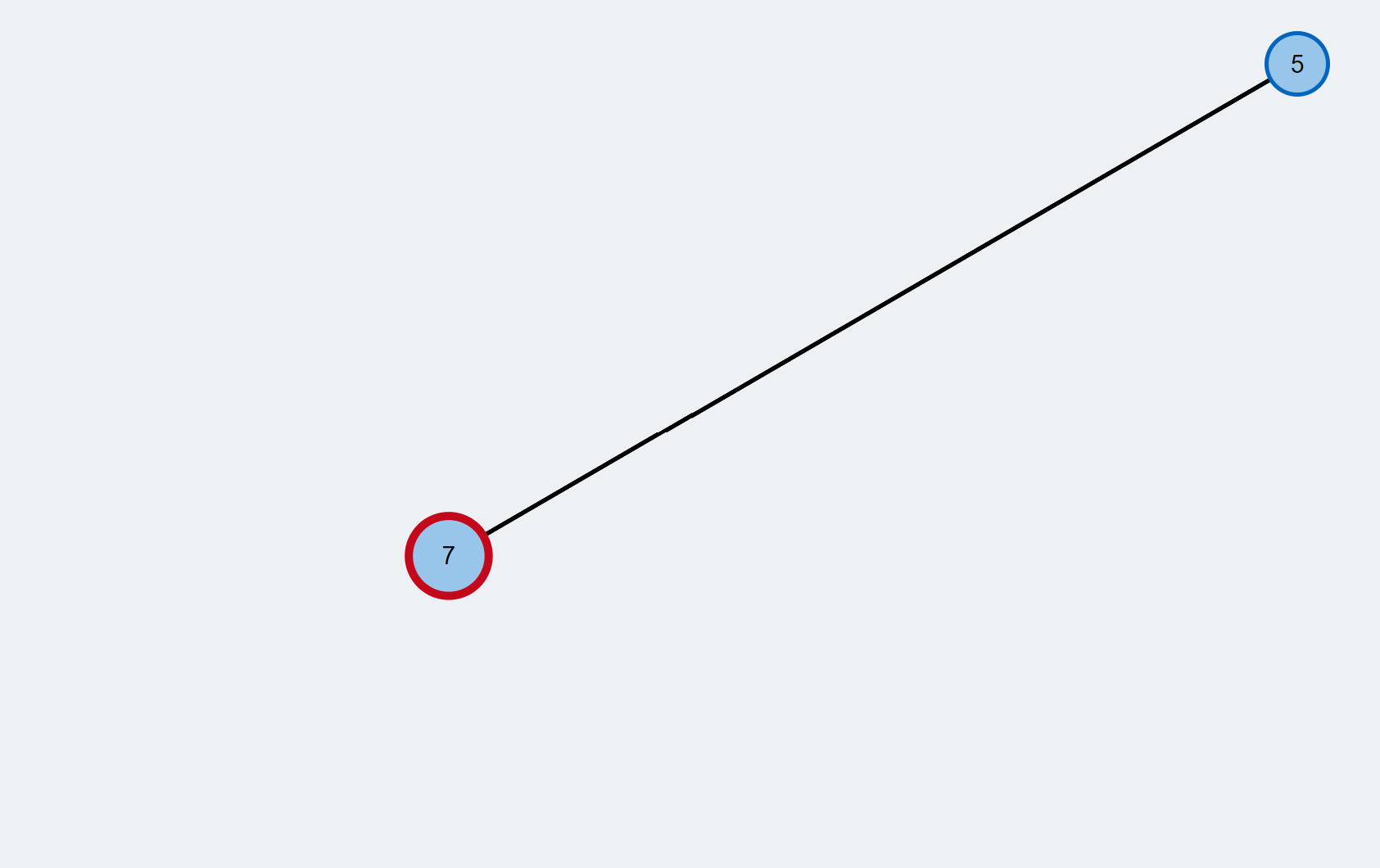
14. Pick the next node from the BFS queue. We call this node the currently active node and color it red. From this node, we will explore its neighbors to look for a free vertex.

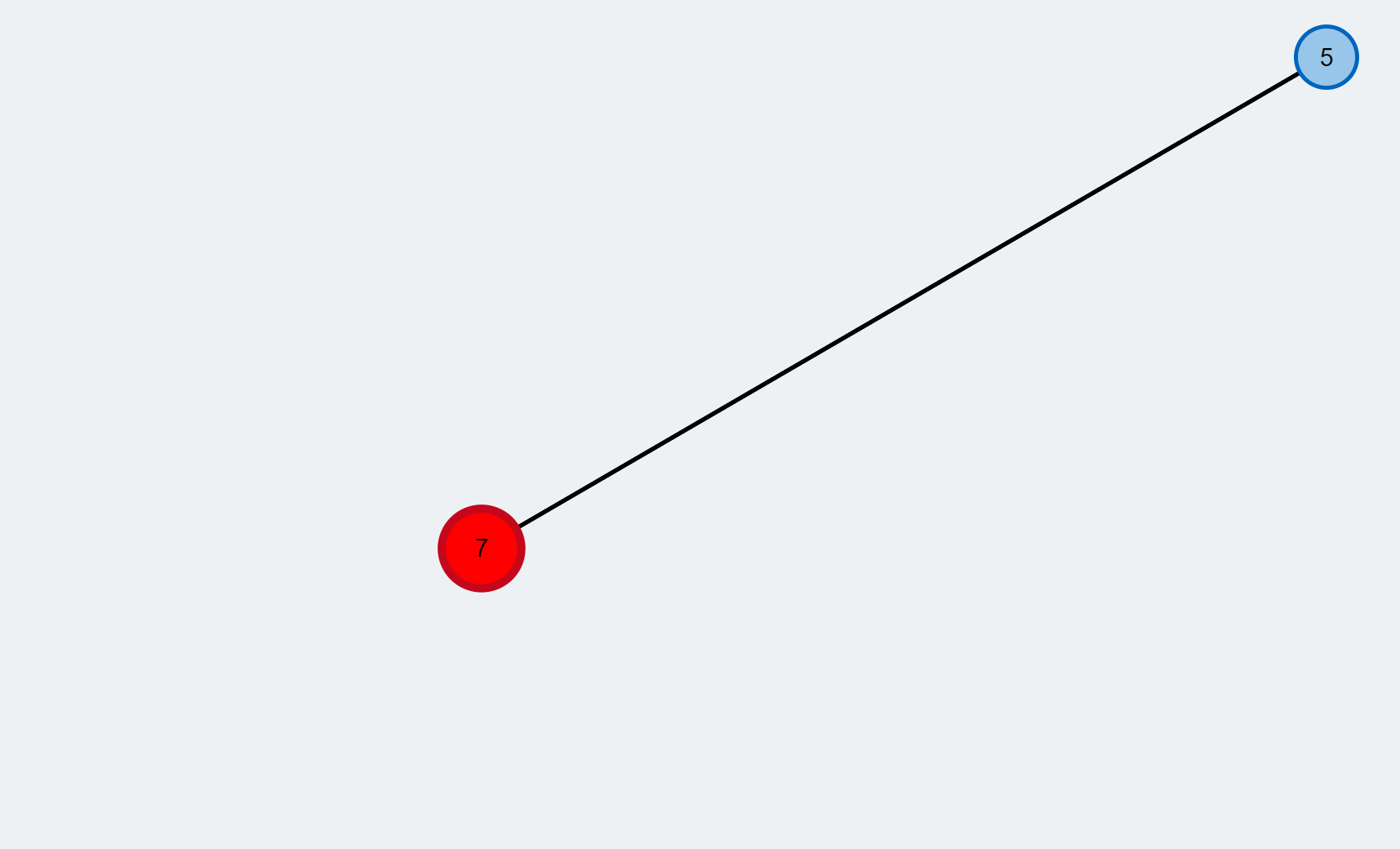
15. We check the next neighbor (orange edge) and find that it is a free vertex (yellow). Thus, there is an augmenting path between the root of the BFS and this vertex.

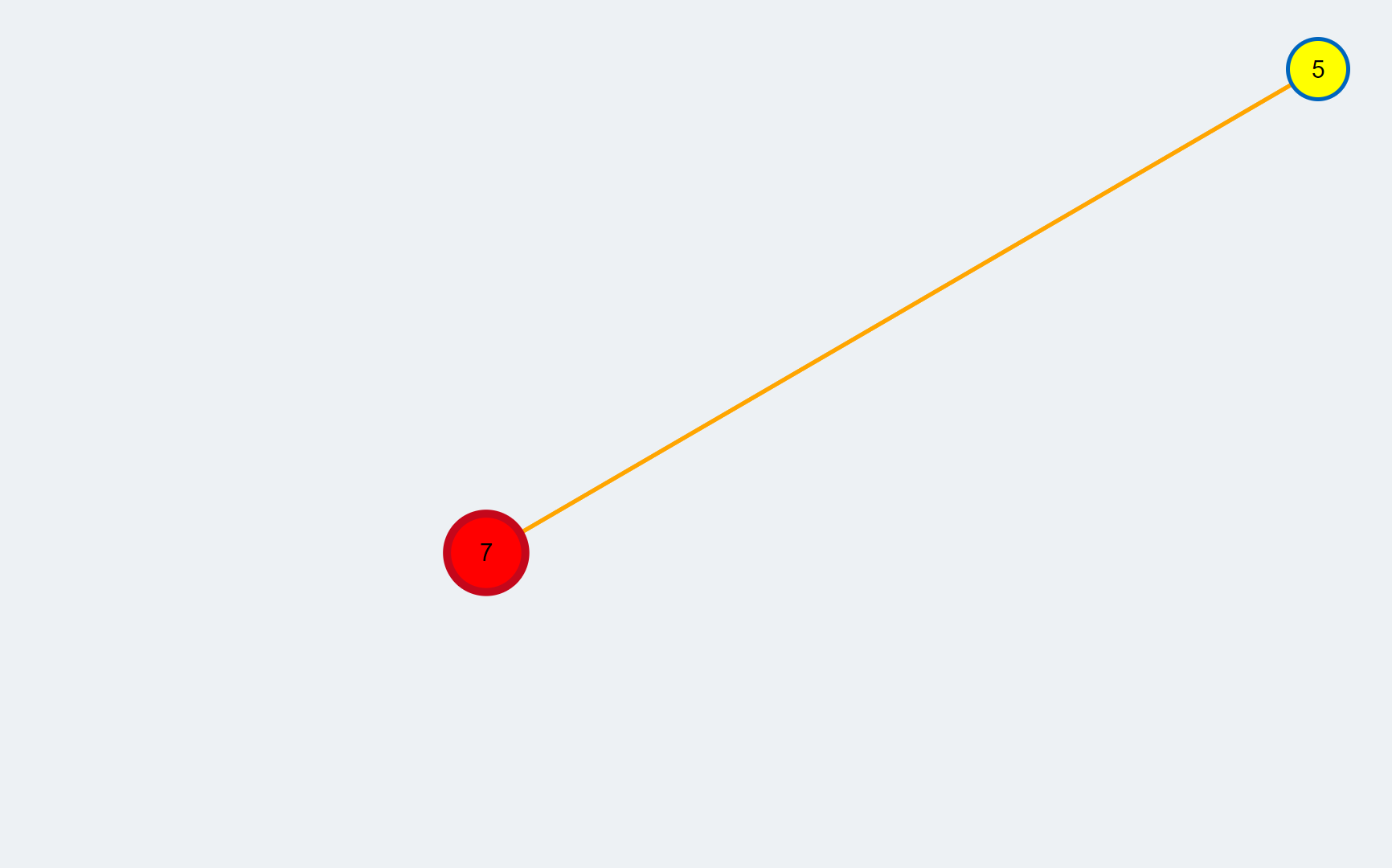
16. The augmenting path is highlighted green. Before improving the matching we have to expand the supernodes contained in the graph.

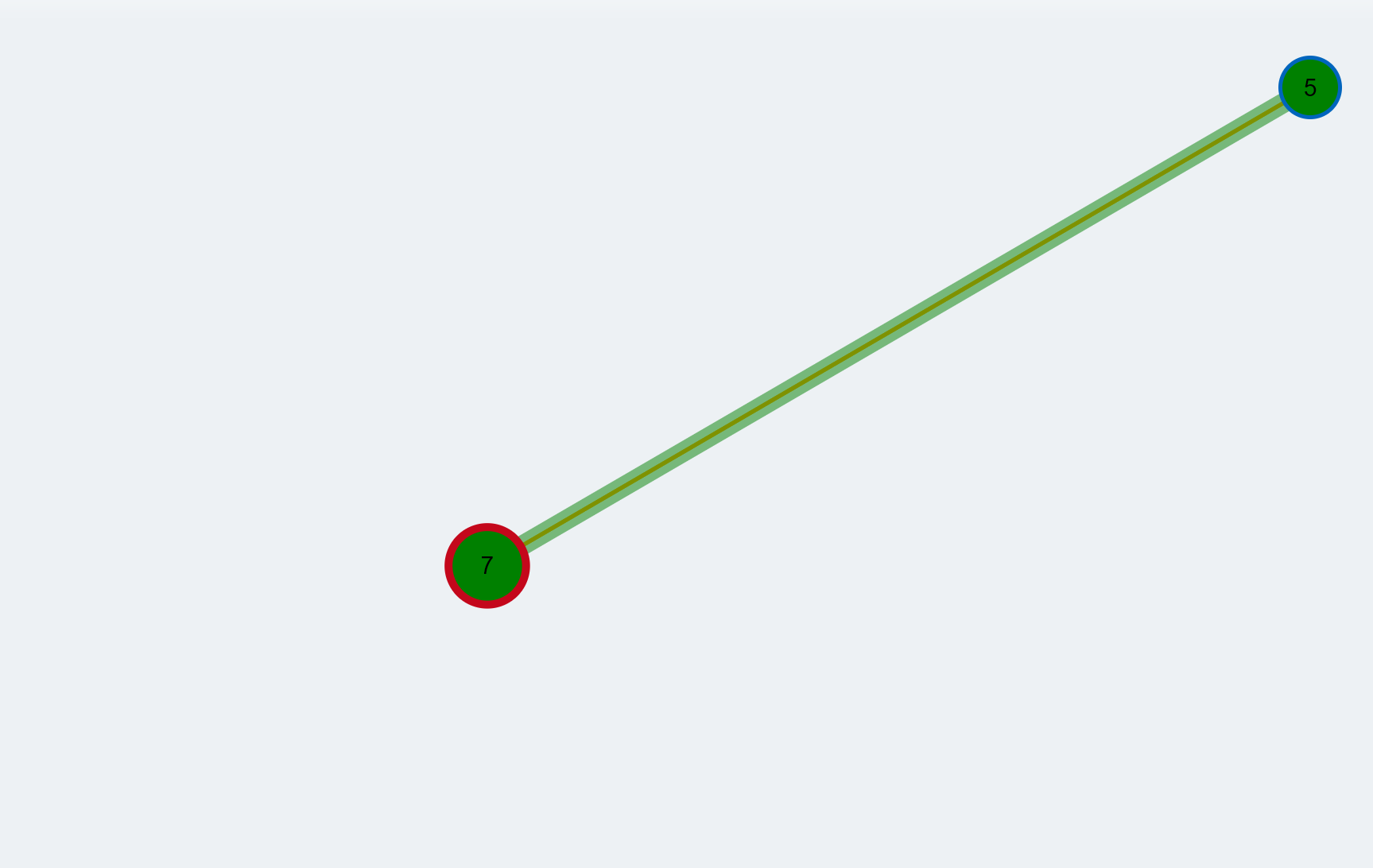
17. After the expansion of all supernodes the augmenting path is fully reconstructed and highlighted green.

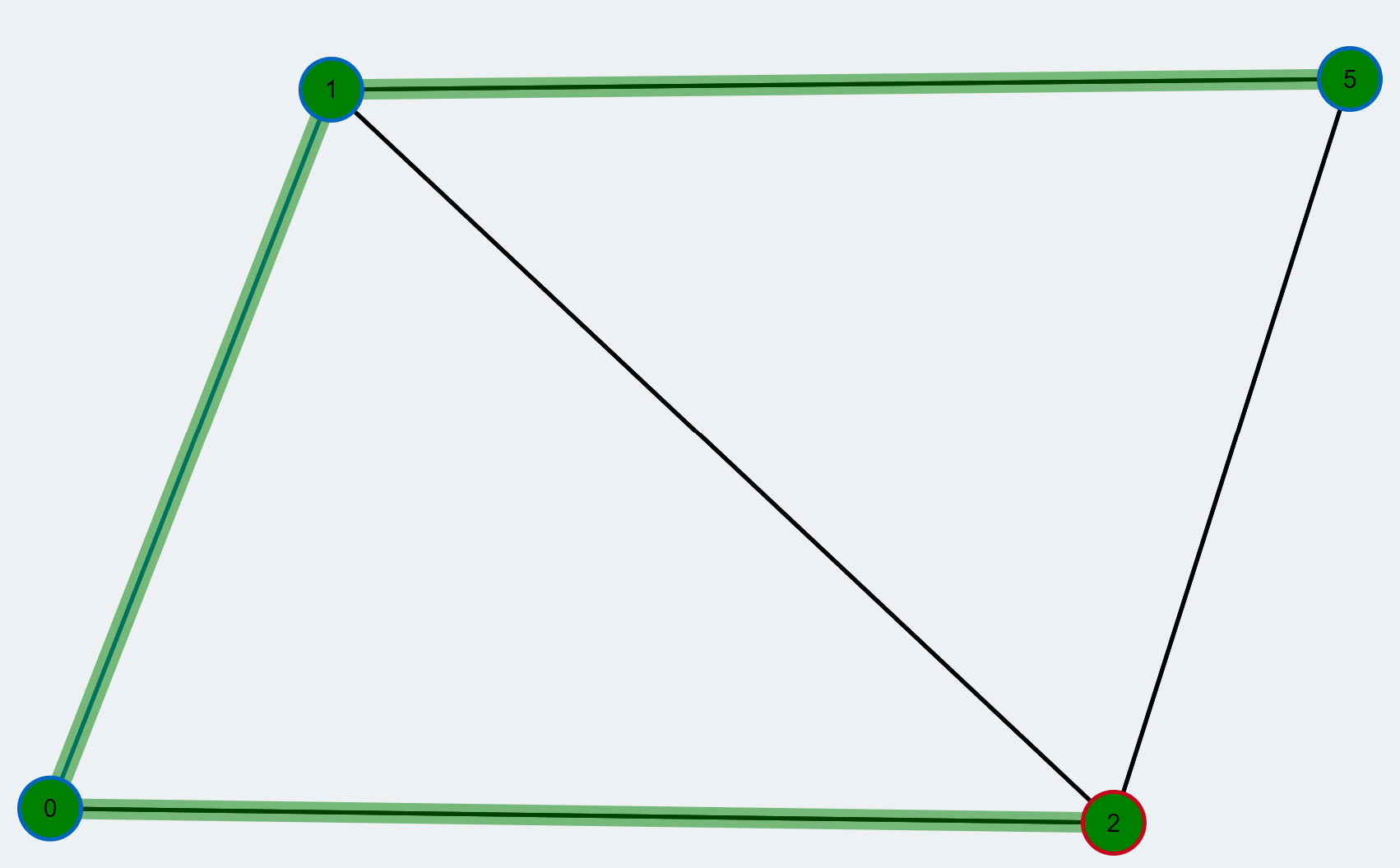
18. The augmenting path is inverted to improve the matching. Inverting an augmenting path means that all unmatched edges along the path are changed to matched ones and vice versa. By doing so, the number of edges contained in the matching increases by 1. The new matching is colored blue.

Formal definition using appropriate notation

Consider an undirected unweighted graph G(V, E), where V and E are the set of vertices and the set of edges respectively. Let M denote the numbers of matchings in the graph G

Given a graph G and a matching M, M is a maximum matching if and only if there exists no M-augmenting path.

Complexity of Algorithm[16]

Three outcomes of Blossom Algorithm:

1. Maximum Matching
2. An Augmenting Path
3. Blossom

In worst case: The total runtime that the algorithm has is O(|E||V|^2) and each iteration takes in O(|E|).

Use in Decision Making for Robotics

One of the important research areas in Robotics where the Blossom Algorithm has been applied extensively is the task allocation problem.

From [1], Consider n robots colored black and m tasks colored gray as shown in the figure. The task allocation problem here can be defined as a bipartite(bigraphs) which are used to study and analyse the robot-task relationships. A Bipartite graph is the one in which the vertices can be divided into two sets such that no two vertices of the same set can be connected by a common edge. The definition of the bipartite graph perfectly explains the scenario here when we have two separate sets one for the robots and other for the tasks and as no two robots be related to each other but robot and tasks. The edges between the robots and the tasks are weighted in order to avoid the random allocation of the tasks to the robots.

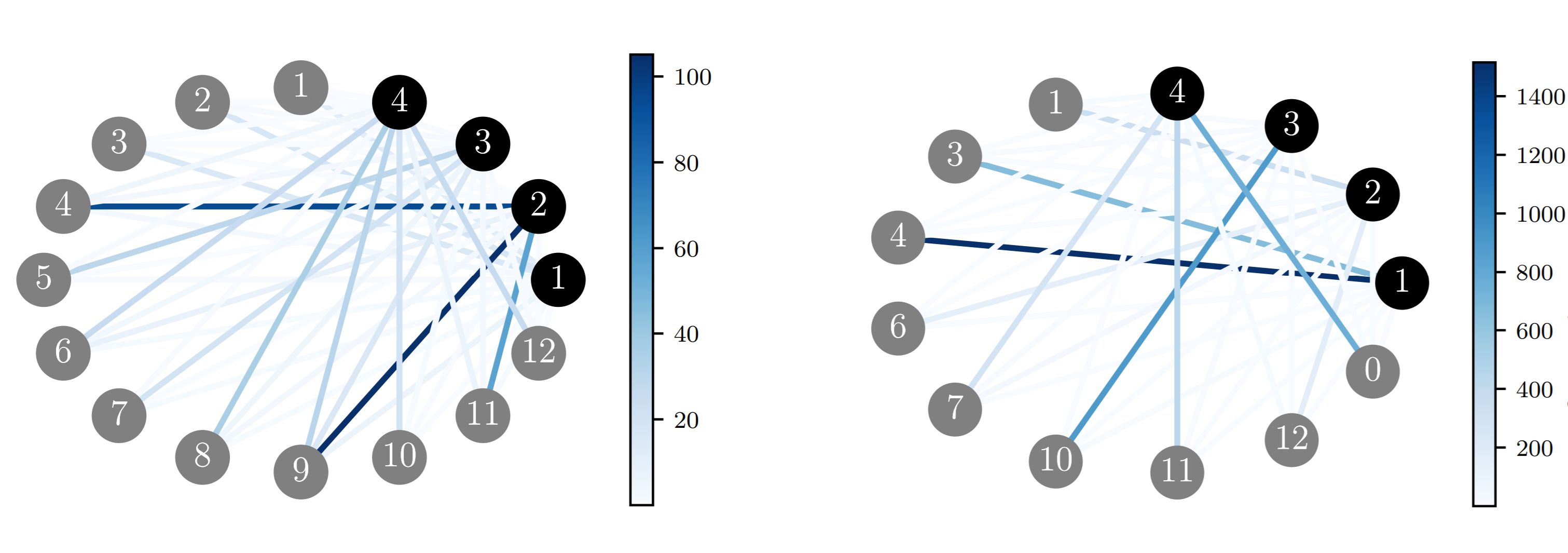
Once the weighted bipartite graph is produced, based on the weights of the edges a matching graph M is constructed which gives the optimized solution.

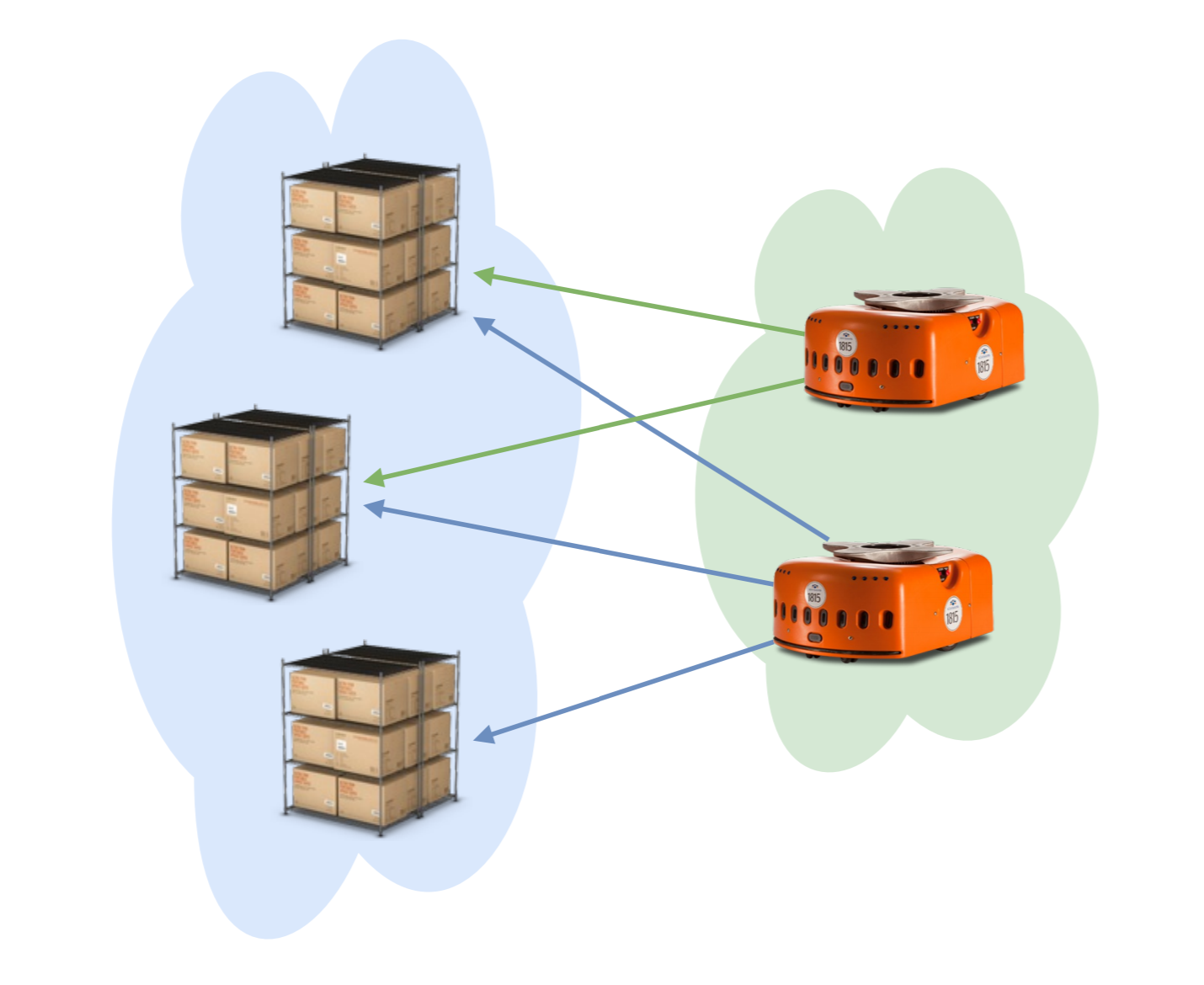
In electronic circuit design applications, the end effector of the manipulators need to design the path such that the vertical motion of the manipulator is minimum. In that case the problem can be formulated as a euclidean path planning algorithm and then the Edmund`s Blossom Algorithm can be used to find the optimal path

Other Applications

Apart from the Robotics Applications such as Task Allocation and Target Tracking. Blossom' Algorithms is used in the solution of combinatorical problems such as the Hall' Marriage Problem and the path problem such as the Hamiltonian Path Problems.

Other areas where the Blossom Matching Algorithm finds its applications are:

• The Assignment Problem
• The oil well drilling problem
• Plotting Street Maps
• Scheduling Problems
• Set Packing Problems

Open research questions

In the robotics research, the blossom algorithm implementation can be optimized by the adoption of distributed parallelization and problem decomposition approaches.

References

1. Ghassemi, Payam, and Chowdhury, Souma. "Decentralized Task Allocation in Multi-Robot Systems via Bipartite Graph Matching Augmented With Fuzzy Clustering." Proceedings of the ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 2A: 44th Design Automation Conference. Quebec City, Quebec, Canada. August 26–29, 2018. V02AT03A014. ASME. https://doi.org/10.1115/DETC2018-86161
2. Edmonds, J. (1965). Paths, Trees, and Flowers. Canadian Journal of Mathematics, 17, 449-467. doi:10.4153/CJM-1965-045-4
3. Blum, N. (2015). Maximum Matching in General Graphs Without Explicit Consideration of Blossoms Revisited. ArXiv, abs/1509.04927.
4. Harold N. Gabow:Data Structures for Weighted Matching and Extensions to b-matching and f-factors. ACM Trans. Algorithms 14(3): 39:1-39:80 (2018)
5. http://www.math.uwaterloo.ca/~bico//papers/cobook_select.pdf
6. http://www.fang.ece.ufl.edu/eel6935/presentation/GraphTheory.pdf
7. Elements of Graph Theory
8. https://www-m9.ma.tum.de/graph-algorithms/matchings-blossom-algorithm/index_en.html
9. https://www.eecs.tufts.edu/~gdicks02/Blossom/Blossom_Algorithm.html
10. http://www.cs.cmu.edu/~anupamg/advalgos15/lectures/lecture08.pdf
11. https://en.wikipedia.org/wiki/Graph_theory#Applications
12. https://en.wikipedia.org/wiki/Bipartite_graph
13. https://people.scs.carleton.ca/~maheshwa/courses/5703COMP/16Fall/Matching-Report.pdf
14. http://web.eecs.utk.edu/~jplank/plank/classes/cs494/494/notes/Edmonds/index.html
15. https://www.cs.tau.ac.il/~zwick/grad-algo-0910/match.pdf
16. https://brilliant.org/wiki/blossom-algorithm/